
POLINOMIOS
A. Introducción
A. a) Definición de polinomios.
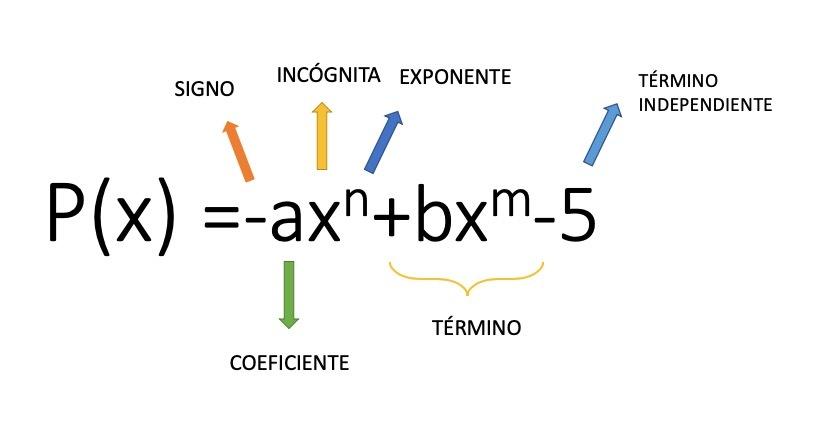
Nota: El grado de un polinomio es el grado del término con el grado más alto en el.
MONOMIO
Es un término de una sola variable.
Ejemplo...
8x^2 , -5x^2 , x^2
BINOMIO
Terminó formado por dos términos o la suma de dos monomios.
Ejemplo...
(34*A + B/23) o (43 A + 1/3 * B ) 2
TRINOMIO
Terminó formado por la suma de tres monomios.
Ejemplo...
x^2 + 2x + 1 o 2a^2 – (a+b) + 3c^3
POLINOMIO
Es un monomio o una suma infinita de monomios.
A. b) Teorema del residuo y el factor.
¿Qué es el teorema del factor y el residuo?
Cuando hablamos de teorema, al menos en matemáticas, nos referimos a preposiciones aceptadas y demostradas que realmente funcionan.
Partiendo desde ese punto, definimos al teorema del factor y el residuo como una ecuación que involucra un polinomio expresado como P(x) que se divide entre en binomio, expresado en un número real (x - a), y el resultado es un residuo que es f(a).
Matemáticamente, este teorema que forma parte del área del algebra con variables como: polinomios, binomios, factores, residuos y divisiones de polinomio. La finalidad de la operación es conocer cuál es el residuo, de haberlo o de formar parte de la operación. Sin tener que efectuar la división.
¿Cuáles son los elementos que influyen en el teorema del factor y el residuo?
Para entender el teorema, primero hay que indagar en elementos que orientan la explicación del problema. Y estos son:
Polinomios
Factor
Residuo
División de polinomios
Explicación del teorema del factor y el residuo
Antes de empezar con la explicación, primero conozcamos el enunciado del teorema del factor y el residuo, diciendo lo siguiente: "Si un polinomio de x, expresado como f(x), se divide entre un número real, expresado como (x - a), se dice que el que el residuo es f(a)."
El significado de este enunciado es que, para encontrar el residuo, hay que realizar una operación con polinomios. Valorando que x es un valor igual a, y a es un valor que es idéntico a x.
De esta forma se obtiene el residuo sin tener que hacer una división, como se mostró en la explicación anterior. Logrando fácilmente a través de la deducción del factor y el contenido de una función real.
Ejemplos del teorema del factor y el residuo
Para profundizar en el tema, te mostraremos algunos ejemplos resueltos enfocados en la demostración matemática de la preposición supuesta en el artículo. Veamos de qué trata.
Ejemplo 1
Consideraremos que el polinomio de este ejemplo es una función expresada como f(x) = x²- 8 x + 6. El objetivo es encontrar el residuo y demostrar el teorema.
El primer paso a realizar es tomar el binomio (x-2) con la finalidad de identificar si existe un residuo dividiéndolo entre polinomio del enunciado. El resultado de esta operación sería -x2 - x2x = x-6 y luego simplificamos la operación hasta que quede de la siguiente forma: -6x + 6. Realizamos una vez otra simplificación, y queda como: -+6 -+12.
Siendo -6 el residuo de este ejemplo.
A. c) División sintetica
*Para hacer una división sintética seguimos los pasos a continuación:
-Y colocar el resultado de "X" (como en la imagen de abajo).
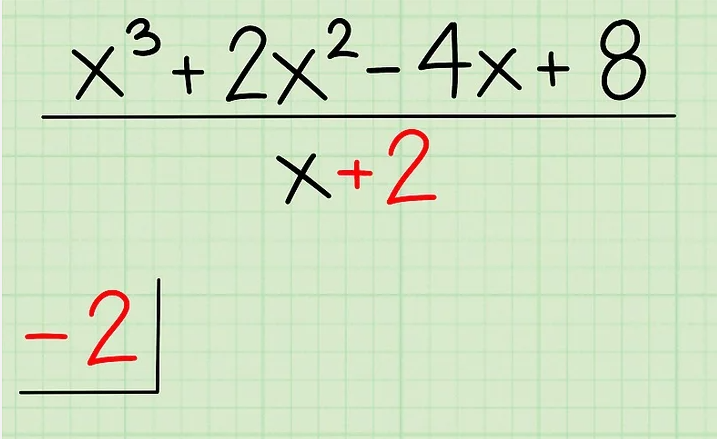
-Escribe todos los coeficientes del dividendo dentro del símbolo de división. Escribe los términos de izquierda a derecha como aparecen. Debe lucir de esta manera: -2| 1 2 -4 8.
-Baja el primer coeficiente. Baja el primer coeficiente, 1, debajo de sí mismo. Hasta ahora tendriamos lo siguiente:
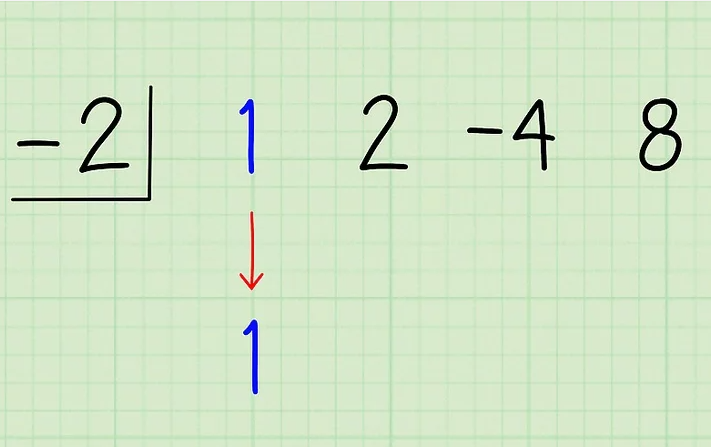
-Multiplica el primer coeficiente por el divisor y colócalo debajo del segundo coeficiente. Simplemente multiplica 1 por -2 para obtener -2 y escribe este producto debajo del segundo término, 2.
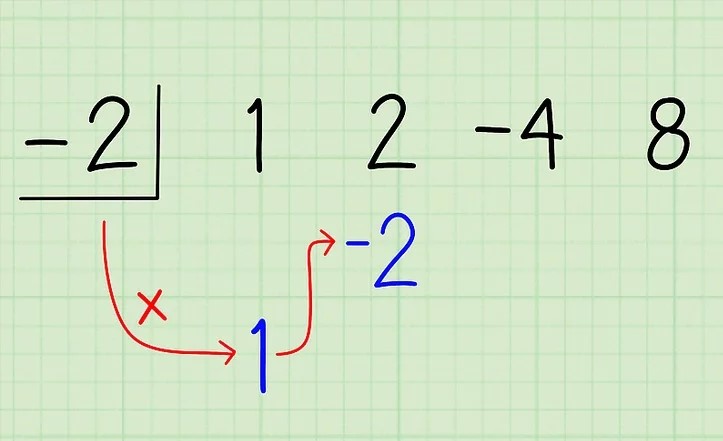
-Suma el segundo coeficiente con el producto y escribe la respuesta debajo del producto. Ahora toma el segundo coeficiente, 2, y súmalo a -2. El resultado es 0. Escribe este resultado debajo de los dos números, de la misma manera que lo harías en una división larga.
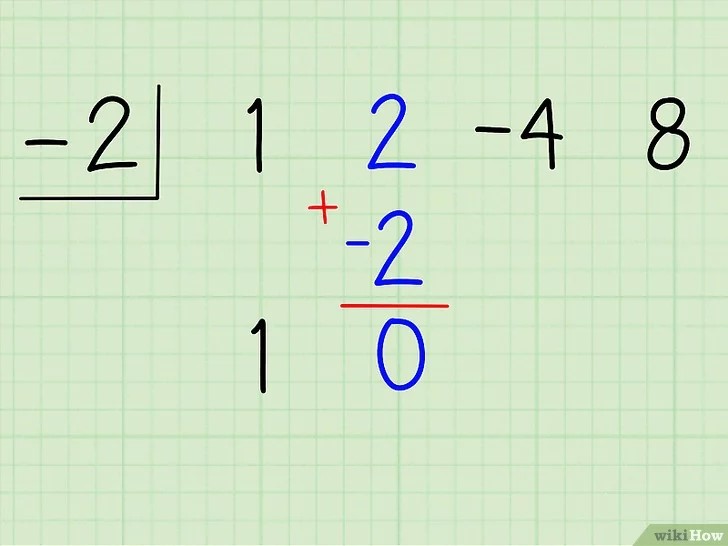
-Multiplica esta suma por el divisor y coloca el resultado debajo del tercer coeficiente. Ahora, toma la suma, 0, y multiplícala por el divisor, -2. El resultado es 0. Coloca este número debajo del 4, el tercer coeficiente.
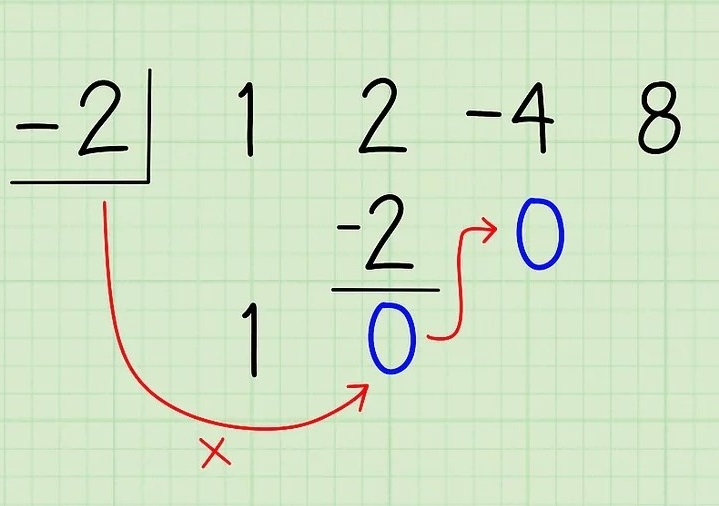
-Suma el producto con el tercer coeficiente y escribe el resultado debajo del producto. Suma 0 y -4 para obtener -4 y escribe la respuesta debajo del 0.
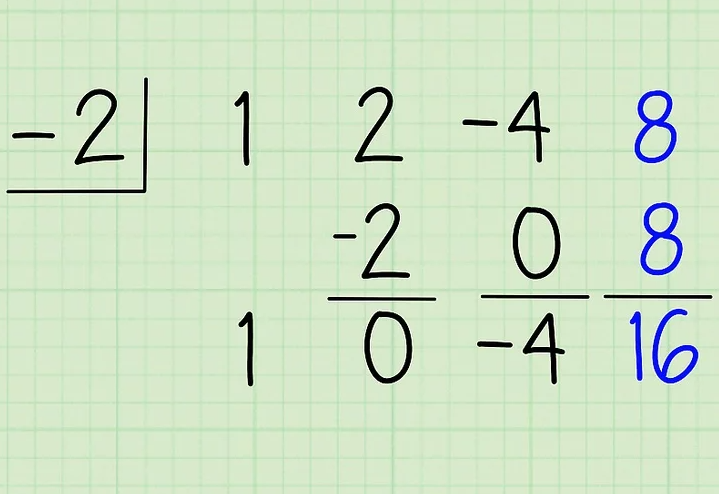
-Multiplica este número por el divisor, escríbelo debajo del último coeficiente, y súmalo al coeficiente. Ahora multiplica -4 por -2 para obtener 8, escribe esta respuesta debajo del cuarto coeficiente, 8, y suma esta respuesta al cuarto coeficiente. 8 + 8 = 16, así que este es tu residuo. Escribe este número debajo del producto.
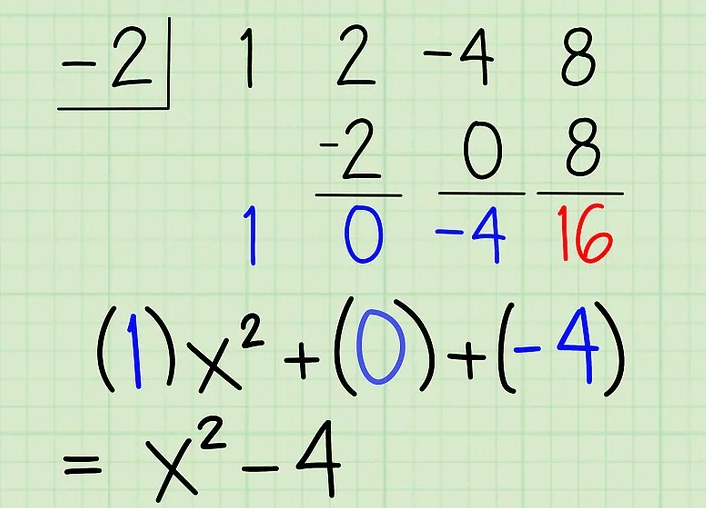
-Coloca cada uno de los nuevos coeficientes al lado de una variable con una potencia inferior a las variables originales correspondientes. En este caso, la primera suma, 1, es colocada al lado de una x a la segunda potencia (una menos que tres). La segunda suma, 0, es colocada al lado de una x, pero el resultado es cero, así que puedes eliminar este término. Y el tercer coeficiente, -4, se convierte en una constante, un número sin variable, debido a que a variable original era x. Puedes escribir un R al lado del 16, porque es el residuo.
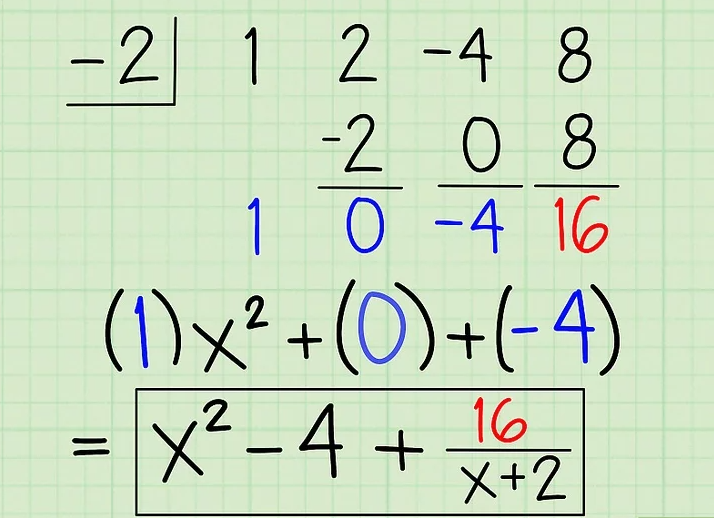
-Escribe la respuesta final. La respuesta final es el nuevo polinomio, x2 - 4, más el residuo, 16, sobre el divisor original, x + 2.
A. d) Representación básica de los polinomios.
A. e) Teorema fundamental del álgebra.
Una función polinomial tiene por lo menos un cero en el conjunto de números complejos .
El teorema fundamental del algebra establece que "Una función polinomial de grado n^th tiene exactamente n ceros en el conjunto de números complejos, contando ceros repetidos ."
Ejemplo:
g ( x ) = x^3 – 2x^2 + 9x – 18
Iguale g ( x ) = 0 y factorice los números complejos para encontrar los ceros.
0 = x^2 ( x – 2) + 9( x – 2)
0 = ( x – 2)( x^2 + 9)
0 = ( x – 2)( x + 3 i )( x – 3 i )
x = 2 o x = –3 i o x = 3 i
Los ceros de la función son 2, 3 i , –3 i
Nota: Los números reales son un subconjunto de los números complejos porque cada número real puede ser escrito en la forma a + bi .
